卡方分布

28 Dec 2020

数学定义

如果 k 个随机变量是相互独立，符合标准正态分布的随机变量（数学期望为 0，方差为 1）。则随机变量的平方和

\[X=\sum_{i=1}^{k} Z_{i}^{2}\]

被称为服从自由度为 k 的卡方分布，记作

\[\begin{array}{l} X \sim \chi^{2}(k) \\ X \sim \chi_{k}^{2} \end{array}\]

在列出卡方分布的性质（概率密度函数以及累计密度函数）之前，需要知道 Gamma 函数。

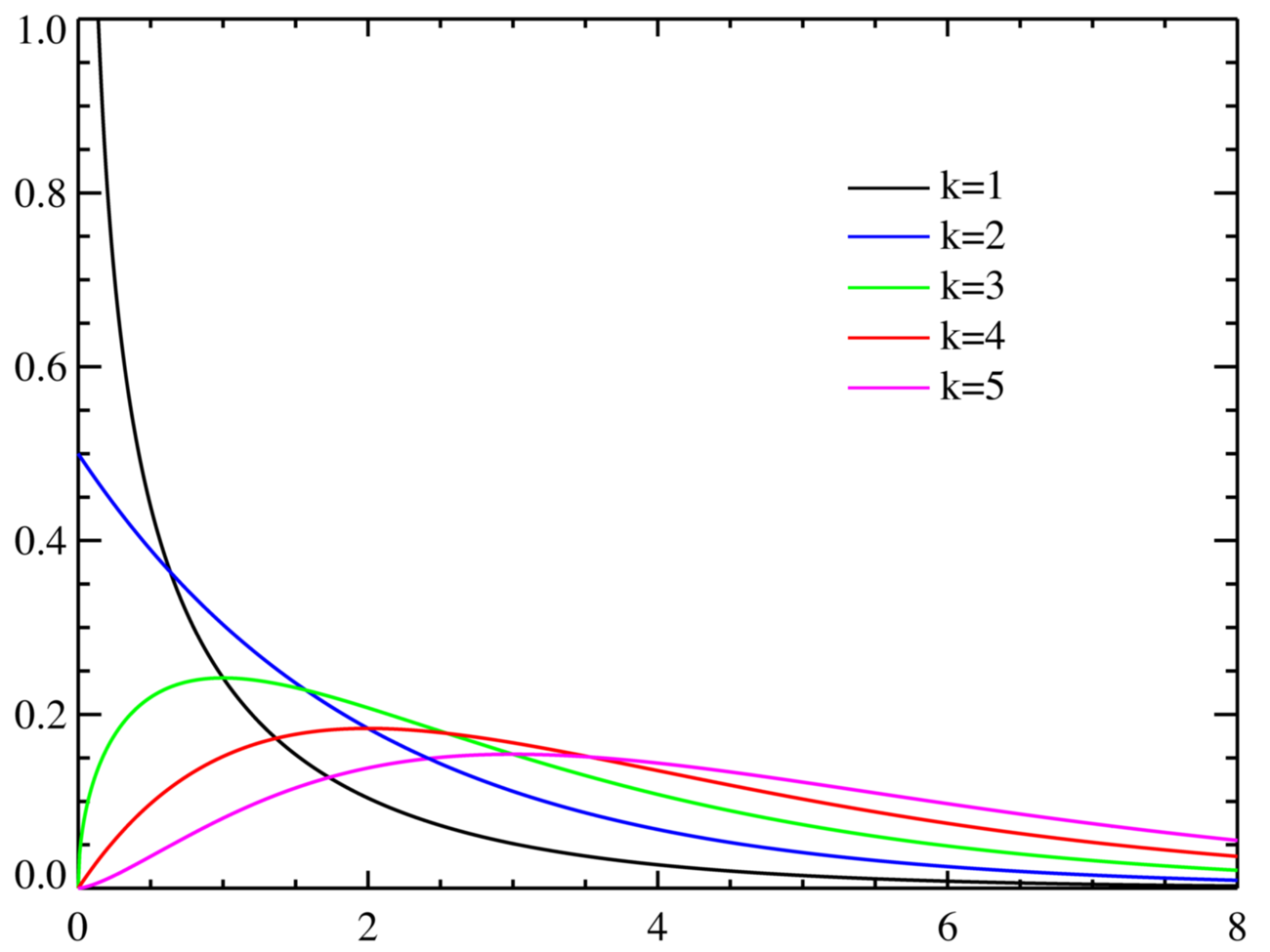
\[f_{k}(x)=\frac{\frac{1}{2}^{\frac{k}{2}}}{\Gamma\left(\frac{k}{2}\right)} x^{\frac{k}{2}-1} e^{\frac{-x}{2}}\]

其中 x >= 0，当 x<=0，f(x)=0，这里 Γ 表示 Gamma 函数。

所谓 Gamma 函数，也叫欧拉第二积分，来源为

下图表示概率密度函数(不同的 k 值)

概率密度函数

\[F_{k}(x)=\frac{\gamma\left(\frac{k}{2}, \frac{x}{2}\right)}{\Gamma\left(\frac{k}{2}\right)}\]

其中 γ(k,z) 为不完全 Γ 函数。

p-value = 1- p_CDF，也就是说 χ2 越大，p-value越小，则可信度越高，通常用 p = 0.05 作为阈值，即 95% 的可信度。

通过 boost::math::quantile(boost::math::chi_squared(dof), 0.95) 即可计算，